2.9 反向传播：全局观

正如我所讲解的，反向传播提出了两个神秘的问题。首先，这个算法真正在干什么？我们已经建立起从输出处的误差被反向传回的画面。但是我们能够更深入一些，构造出一种更加深刻的直觉来解释所有这些矩阵和向量乘法么？第二神秘点就是，某人为什么能发现这个反向传播？跟着一个算法跑一遍甚至能够理解证明算法可以运行这是一回事。这并不真的意味着你理解了这个问题到一定程度，能够发现这个算法。是否有一个推理的思路可以指引你发现反向传播算法？本节，我们来探讨一下这两个谜题。

为了提升我们关于算法究竟做了什么的直觉，假设我们已经对一些网络中的 $w_{jk}^l$ 做一点小小的变动 $\Delta w_{jk}^l$：

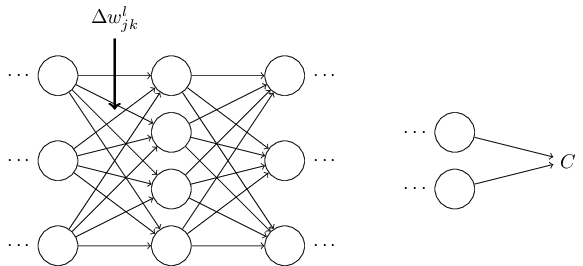
这个改变会导致在输出激活值上的相应改变：

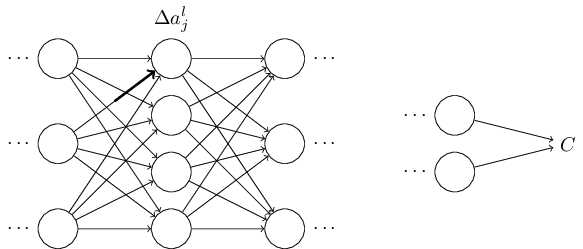
然后，会产生对下一层所有激活值的改变：

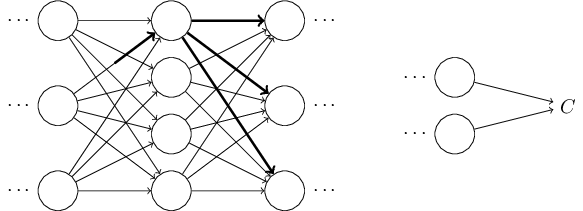
接着，这些改变都将影响到一个个下一层，到达输出层，最终影响代价函数：

所以代价函数 $\Delta C$ 改变和 $\Delta w_{jk}^l$ 就按照下面的公式关联起来了：

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk} \label{eq:47}\tag{47} \end{eqnarray}$

这给出了一种可能的计算 $\frac{\partial C}{\partial w_{jk}^l}$ 的方法其实是细致地追踪一个 $w_{jk}^l$ 的微小变化如何导致 $C$ 中的变化值。如果我们可以做到这点，能够精确地使用易于计算的量来表达每种关系，那么我们就能够计算 $\partial C / \partial w^l_{jk}$ 了。

我们尝试一下这个方法。$\Delta w_{jk}^l$ 导致了在 $l^{th}$ 层 $j^{th}$ 神经元的激活值的变化 $\Delta a_j^l$。这个变化由下面的公式给出：

$\begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \label{eq:48}\tag{48} \end{eqnarray}$

$\Delta a_j^l$ 的变化将会导致下一层 $(l+1)^{\rm th}$ 的所有激活值的变化。我们聚焦到其中一个激活值上看看影响的情况，不妨设 $a_q^{l+1}$，

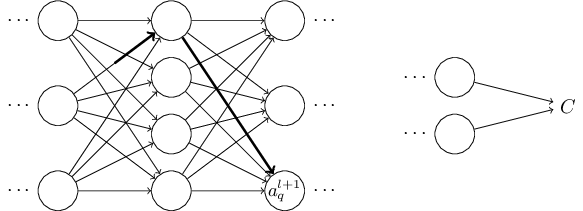
实际上，这会导致下面的变化：

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \Delta a^l_j \label{eq:49}\tag{49} \end{eqnarray}$

将其代入方程 (48)，我们得到：

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \label{eq:50}\tag{50} \end{eqnarray}$

当然，这个变化 $\Delta a^{l+1}_q$ 又会去下一层的激活值。实际上，我们可以想象出一条从 $w_{jk}^l$ 到 $C$ 的路径，然后每个激活值的变化会导致下一层的激活值的变化，最终是输出层的代价的变化。假设激活值的序列如下 $a_j^l, a_q^{l+1},...,a_n^{L-1},a_m^{L}$，那么结果的表达式就是

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \label{eq:51}\tag{51} \end{eqnarray}$

我们已经对每个经过的神经元设置了一个 $\partial a/\partial a$ 这种形式的项，还有输出层的 $\partial C/\partial a_m^L$。这表示除了 $C$ 的改变由于网络中这条路径上激活值的变化。当然，整个网络中存在很多 $w_{jk}^l$ 可以传播而影响代价函数的路径，这里我们就看其中一条。为了计算 $C$ 的全部改变，我们就需要对所有可能的路径进行求和，即，

$\begin{eqnarray} \Delta C \approx \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \label{eq:52}\tag{52} \end{eqnarray}$

这里我们对路径中所有可能的中间神经元选择进行求和。对比 (47) 我们有

$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \label{eq:53}\tag{53} \end{eqnarray}$

现在公式 (53) 看起来相当复杂。但是，这里其实有一个相当好的直觉上的解释。我们用这个公式计算 $C$ 关于网络中一个权重的变化率。而这个公式告诉我们的是：两个神经元之间的连接其实是关联与一个变化率因子，这仅仅是一个神经元的激活值相对于其他神经元的激活值的偏导数。从第一个权重到第一个神经元的变化率因子是 $\partial a_j^l/\partial w_{jk}^l$。路径的变化率因子其实就是这条路径上的众多因子的乘积。而整个的变化率 $\partial C/\partial w_{jk}^l$ 就是对于所有可能的从初始权重到最终输出的代价函数的路径的变化率因子的和。针对某一个路径，这个过程解释如下，

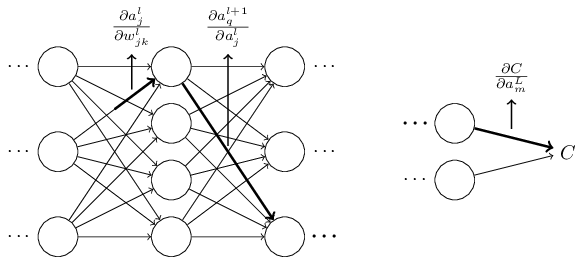
我们到现在所给出的东西其实是一种启发式的观点，一种思考权重变化对网络行为影响的方式。让我们给出关于这个观点应用的一些流程建议。首先，你可以推导出公式 (53) 中所有单独的偏导数显式表达式。只是一些微积分的运算。完成这些后，你可以弄明白如何用矩阵运算写出对所有可能的情况的求和。这项工作会比较乏味，需要一些耐心，但不用太多的洞察。完成这些后，就可以尽可能地简化了，最后你发现，自己其实就是在做反向传播！所以你可以将反向传播想象成一种计算所有可能的路径变化率的求和的方式。或者，换句话说，反向传播就是一种巧妙地追踪权重（和偏置）微小变化的传播，抵达输出层影响代价函数的技术。

现在我不会继续深入下去。因为这项工作比较无聊。如果你想挑战一下，可以尝试去做。即使你不去尝试，我也希望这种思维方式可以让你能够更好地理解反向传播。

那其他的一些神秘的特性呢 —— 反向传播如何在一开始被发现的？实际上，如果你跟随我刚刚给出的观点，你其实是可以发现反向传播的一种证明的。不幸的是，证明会比本章前面介绍的证明更长和更加的复杂。那么，前面那个简短（却更加神秘）的证明如何被发现的？当你写出来所有关于长证明的细节后，你会发现其实里面包含了一些明显的可以进行改进的地方。然后你进行一些简化，得到稍微简短的证明，写下来。然后又能发现一些更加明显的简化。经过几次迭代证明改进后，你会发现最终的简单却看起来奇特的证明⁶，因为你移除了很多构造的细节了！老实告诉你，其实最早的证明的出现也不是太过神秘的事情。因为那只是很多对简化证明的艰辛工作的积累。

⁶. 需要一个巧妙的步骤。在方程 (53) 中的中间变量是类似 $a_q^{l+1}$ 的激活值。巧妙之处是改用加权的输入，例如 $z^{l+1}_q$，作为中间变量。如果你想不到这个主意，而是继续使用激活值 $a_q^{l+1}$，你得到的证明最后会比本章前面给出的证明稍微复杂些。 ↩