1.3 神经网络的架构
在下一节我会介绍一个神经网络,我们可以用它来很好地分类手写数字。准备进入下一节时,解释一些可以让我们命名网络中不同部分的术语是很有帮助的。假设我们有这样的网络:
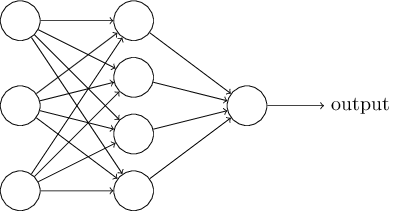
前面提过,这个网络中最左边的称为输入层,其中的神经元称为输入神经元。最右边的,即输出层包含有输出神经元,在本例中,输出层只有一个神经元。中间层,既然这层中的神经元既不是输入也不是输出,则被称为隐藏层。“隐藏”这一术语也许听上去有些神秘 —— 我第一次听到这个词,以为它必然有一些深层的哲学或数学涵意 —— 但它实际上仅仅意味着“既非输入也非输出”。上面的网络仅有一个隐藏层,但有些网络有多个隐藏层。例如,下面的四层网络有两个隐藏层:
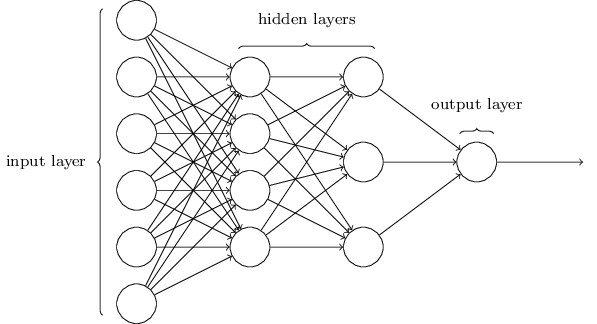
有些令人困惑的是,由于历史的原因,尽管是由 S 型神经元而不是感知器构成,这种多层网络有时被称为多层感知器或者 MLP。在这本书中我不会使用 MLP 这个术语,因为我认为这会引起混淆,但这里想提醒你它的存在。
设计网络的输入输出层通常是比较直接的。例如,假设我们尝试确定一张手写数字的图像上是否写的是“”。很自然地,我们可以将图片像素的强度进行编码作为输入神经元来设计网络。如果图像是一个 的灰度图像,那么我们会需要 个输入神经元,每个强度取 和 之间合适的值。输出层只需要包含一个神经元,当输出值小于 时表示 “输入图像不是一个 ”,大于 的值表示 “输入图像是一个 ”。
相比于神经网络中输入输出层的直观设计,隐藏层的设计则堪称一门艺术。特别是,通过一些简单的经验法则来总结隐藏层的设计流程是不可行的。相反,神经网络的研究人员已经为隐藏层开发了许多设计最优法则,这有助于网络的行为能符合人们期望的那样。例如,这些法则可以用于帮助权衡隐藏层数量和训练网络所需的时间开销。在本书后面我们会碰到几个这样的设计最优法则。
目前为止,我们讨论的神经网络,都是以上一层的输出作为下一层的输入。这种网络被称为前馈神经网络。这意味着网络中是没有回路的 —— 信息总是向前传播,从不反向回馈。如果确实有回路,我们最终会有这样的情况: 函数的输入依赖于输出。这将难于理解,所以我们不允许这样的环路。
然而,也有一些人工神经网络的模型,其中反馈环路是可行的。这些模型被称为递归神经网络。这种模型的设计思想,是具有休眠前会在一段有限的时间内保持激活状态的神经元。这种激活状态可以刺激其它神经元,使其随后被激活并同样保持一段有限的时间。这样会导致更多的神经元被激活,随着时间的推移,我们得到一个级联的神经元激活系统。因为一个神经元的输出只在一段时间后而不是即刻影响它的输入,在这个模型中回路并不会引起问题。
递归神经网络比前馈网络影响力小得多,部分原因是递归网络的学习算法(至少目前为止)不够强大。但是递归网络仍然很有吸引力。它们原理上比前馈网络更接近我们大脑的实际工作。并且递归网络能解决一些重要的问题,这些问题如果仅仅用前馈网络来解决,则更加困难。然而为了篇幅,本书将专注于使用更广泛的前馈网络。