1.7 迈向深度学习

虽然我们的神经网络给出了令人印象深刻的表现，但这样的表现带有几分神秘。网络中的权重和偏置是被自动发现的。这意味着我们不能立即解释网络怎么做的、做了什么。我们能否找到一些方法来理解我们的网络通过什么原理分类手写数字？并且，在知道了这些原理后，我们能做得更好吗？

为了让这些问题更具体，我们假设数十年后神经网络引发了人工智能（AI）。到那个时候，我们能明白这种智能网络的工作机制吗？或许，因为有着自动学习得到的权重和偏置，这些是我们无法理解的，这样的神经网络对我们来说是不透明的。在人工智能的早期研究阶段，人们希望在构建人工智能的努力过程中，也同时能够帮助我们理解智能背后的机制，以及人类大脑的运转方式。但结果可能是我们既不能够理解大脑的机制，也不能够理解人工智能的机制。

为解决这些问题，让我们重新思考一下我在本章开始时所给的人工神经元的解释，作为一种衡量证据的方法。假设我们要确定一幅图像是否显示有人脸⁸：

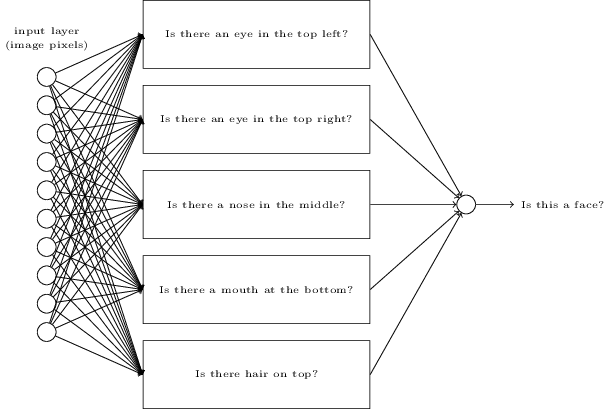
我们可以用解决手写识别问题的相同方式来攻克这个问题 —— 网络的输入是图像中的像素，网络的输出是一个单个的神经元用于表明“是的，这是一张脸”或“不，这不是一张脸”。

假设我们就采取了这个方法，但接下来我们先不去使用一个学习算法。而是去尝试亲手设计一个网络，并为它选择合适的权重和偏置。我们要怎样做呢？暂时先忘掉神经网络，我们受到启发的一个想法是将这个问题分解成子问题：图像的左上角有一个眼睛吗？右上角有一个眼睛吗？中间有一个鼻子吗？下面中央有一个嘴吗？上面有头发吗？诸如此类。

如果一些问题的回答是“是”，或者甚至仅仅是“可能是”，那么我们可以作出结论这个图像可能是一张脸。相反地，如果大多数这些问题的答案是“不是”，那么这张图像可能不是一张脸。

当然，这仅仅是一个粗略的想法，而且它存在许多缺陷。也许有个人是秃头，没有头发。也许我们仅仅能看到脸的部分，或者这张脸是有角度的，因此一些面部特征是模糊的。不过这个想法表明了如果我们能够使用神经网络来解决这些子问题，那么我们也许可以通过将这些解决子问题的网络结合起来，构成一个人脸检测的神经网络。下图是一个可能的结构，其中的方框表示子网络。注意，这不是一个人脸检测问题的现实的解决方法，而是为了帮助我们构建起网络如何运转的直观感受。下图是这个网络的结构：

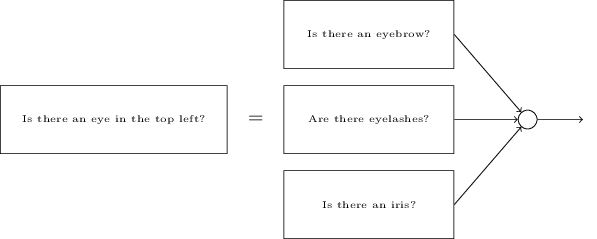
子网络也可以被继续分解，这看上去很合理。假设我们考虑这个问题：“左上角有一个眼睛吗？”。 这个问题可以被分解成这些子问题：“有一个眉毛吗？”，“有睫毛吗？”，“有虹膜吗？”，等等。当然这些问题也应该包含关于位置的信息 —— 诸如“在左上角有眉毛，上面有虹膜吗？” —— 但是让我们先保持简单。回答问题“左上角有一个眼睛吗？”的网络能够被分解成：

这些子问题也同样可以继续被分解，并通过多个网络层传递得越来越远。最终，我们的子网络可以回答那些只包含若干个像素点的简单问题。举例来说，这些简单的问题可能是询问图像中的几个像素是否构成非常简单的形状。这些问题就可以被那些与图像中原始像素点相连的单个神经元所回答。

最终的结果是，我们设计出了一个网络，它将一个非常复杂的问题 —— 这张图像是否有一张人脸 —— 分解成在单像素层面上就可回答的非常简单的问题。它通过一系列多层结构来完成，在前面的网络层，它回答关于输入图像非常简单明确的问题，在后面的网络层，它建立了一个更加复杂和抽象的层级结构。包含这种多层结构 —— 两层或更多隐藏层 —— 的网络被称为深度神经网络。

当然，我没有提到如何去递归地分解成子网络。手工设计网络中的权重和偏置无疑是不切实际的。取而代之的是，我们希望使用学习算法来让网络能够自动从训练数据中学习权重和偏差 —— 这样，形成一个概念的层次结构。80 年代和 90 年代的研究人员尝试了使用随机梯度下降和反向传播来训练深度网络。不幸的是，除了一些特殊的结构，他们并没有取得很好的效果。虽然网络能够学习，但是学习速度非常缓慢，不适合在实际中使用。

自 2006 年以来，人们已经开发了一系列技术使深度神经网络能够学习。这些深度学习技术基于随机梯度下降和反向传播，并引进了新的想法。这些技术已经使更深（更大）的网络能够被训练 —— 现在训练一个有 5 到 10 层隐藏层的网络都是很常见的。而且事实证明，在许多问题上，它们比那些浅层神经网络，例如仅有一个隐藏层的网络，表现的更加出色。当然，原因是深度网络能够构建起一个复杂的概念的层次结构。这有点像传统编程语言使用模块化的设计和抽象的思想来创建复杂的计算机程序。将深度网络与浅层网络进行对比，有点像将一个能够进行函数调用的程序语言与一个不能进行函数调用的精简语言进行对比。抽象在神经网络中的形式和传统的编程方式相比不同，但它同样重要。

⁸. 照片来源： 1. Ester Inbar. 2. 未知. 3. NASA, ESA, G. Illingworth, D. Magee, and P. Oesch (University of California, Santa Cruz), R. Bouwens (Leiden University), and the HUDF09 Team. 点击序号查看更多细节。 ↩