2.4 反向传播的四个基本方程

反向传播其实是对权重和偏置变化影响代价函数过程的理解。最终极的含义其实就是计算偏导数 $\partial C/\partial w_{jk}^l$ 和 $\partial C/\partial b_j^l$。但是为了计算这些值，我们首先引入一个中间量，$\delta_j^l$，这个我们称为在 $l^{th}$ 层第 $j^{th}$ 个神经元上的误差。

反向传播将给出计算误差 $\delta_j^l$ 的流程，然后将其关联到计算 $\partial C/\partial w_{jk}^l$ 和 $\partial C/\partial b_j^l$ 上

为了理解误差是如何定义的，假设在神经网络上有一个调皮鬼：

这个调皮鬼在 $l$ 层的第 $j^{th}$ 个神经元上。当输入进来时，调皮鬼对神经元的操作进行搅局。他会增加很小的变化 $\Delta z_j^l$ 在神经元的带权输入上，使得神经元输出由 $\sigma(z_j^l)$ 变成 $\sigma(z_j^l + \Delta z_j^l)$。这个变化会向网络后面的层进行传播，最终导致整个代价产生 $\frac{\partial C}{\partial z_j^l} \Delta z_j^l$ 的改变。

现在，这个调皮鬼变好了，试着帮助你来优化代价，它试着找到可以让代价更小的 $\Delta z_j^l$。假设 $\frac{\partial C}{\partial z_j^l}$ 有一个很大的值（或正或负）。那么这个调皮鬼可以通过选择与 $\frac{\partial C}{\partial z_j^l}$ 相反符号的 $\Delta z_j^l$ 来降低代价。相反，如果 $\frac{\partial C}{\partial z_j^l}$ 接近 $0$，那么调皮鬼并不能通过扰动带权输入 $z_j^l$ 来改善太多代价。在调皮鬼看来，这时候神经元已经很接近最优了²。所以这里有一种启发式的认识，$\frac{\partial C}{\partial z_j^l}$ 是神经元的误差的度量。

按照上面的描述，我们定义 $l$ 层的第 $j^{th}$ 个神经元上的误差 $\delta_j^l$ 为：

$\begin{eqnarray} \delta^l_j \equiv \frac{\partial C}{\partial z^l_j} \label{eq:29}\tag{29} \end{eqnarray}$

按照我们通常的惯例，我们使用 $\delta^l$ 表示关联于 $l$ 层的误差向量。反向传播会提供给我们一种计算每层的 $\delta^l$ 的方法，然后将这些误差和最终我们需要的量 $\partial C/\partial w_{jk}^l$ 和 $\partial C/\partial b_j^l$ 联系起来。

你可能会想知道为何这个调皮鬼在改变带权输入 $z_j^l$。把它想象成改变输出激活值 $a_j^l$ 肯定会更加自然，然后就使用 $\frac{\partial C}{\partial a_j^l}$ 作为度量误差的方法了。实际上，如果你这样做的话，其实和下面要讨论的差不多。但是看起来，前面的方法会让反向传播在代数运算上变得比较复杂。所以我们坚持使用 $\delta_j^l = \partial C / \partial z_j^l$ 作为误差的度量³。

解决方案： 反向传播基于四个基本方程。这些方程给我们一种计算误差 $\delta^l$ 和代价函数梯度的方法。我列出这四个方程。但是需要注意：你不需要一下子能够同时理解这些公式。希望越大失望越大。实际上，反向传播方程内容很多，完全理解这些需要花费充分的时间和耐心，需要一步一步地深入理解。而好的消息是，这样的付出回报巨大。所以本节对这些内容的讨论仅仅是一个帮助你正确掌握这些方程的起步。

下面简要介绍我们的探讨这些公式的计划：首先给出这些公式的简短证明以解释他们的正确性；然后以伪代码的方式给出这些公式的算法形式，并展示这些伪代码如何转化成真实的可执行的 Python 代码；在本章的最后，我们会发展出一个关于反向传播方程含义的直觉画面，以及人们如何能够从零开始发现这个规律。按照此法，我们会不断地提及这四个基本方程，随着你对这些方程理解的加深，他们会看起来更加舒服，甚至是美妙和自然的。

输出层误差的方程，$\delta^L$： 每个元素定义如下：

$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \label{eq:bp1}\tag{BP1} \end{eqnarray}$

这是一个非常自然的表达式。右式第一个项 $\partial C/\partial a_j^L$ 表示代价随着$j^{th}$ 输出激活值的变化而变化的速度。假如 $C$ 不太依赖一个特定的输出神经元 $j$，那么 $\delta_j^L$ 就会很小，这也是我们想要的效果。右式第二项 $\sigma'(z_j^L)$ 刻画了在 $z_j^L$ 处激活函数 $\sigma$ 变化的速度。

注意到在 (BP1) 中的每个部分都是很好计算的。特别地，我们在计算网络行为时计算 $z_j^L$，这仅仅需要一点点额外工作就可以计算 $\sigma'(z_j^L)$。当然$\partial C/\partial a_j^L$ 依赖于代价函数的形式。然而，给定了代价函数，计算$\partial C/\partial a_j^L$ 就没有什么大问题了。例如，如果我们使用二次函数，那么 $C = \frac{1}{2} \sum_j(y_j-a_j)^2$，所以 $\partial C/\partial a_j^L = (a_j - y_j)$，这其实很容易计算。

方程 (BP1) 对 $\delta^L$ 来说是个按分量构成的表达式。这是一个非常好的表达式，但不是我们期望的用矩阵表示的形式。但是，以矩阵形式重写方程其实很简单，

$\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L) \label{eq:bp1a}\tag{BP1a} \end{eqnarray}$

这里 $\nabla_a C$ 被定义成一个向量，其元素是偏导数 $\partial C/\partial a_j^L$。你可以将 $\nabla_a C$ 看成是 $C$ 关于输出激活值的改变速度。方程 (BP1) 和方程 (BP1a) 的等价也是显而易见的，所以现在开始，我们会用 (BP1) 表示这两个方程。举个例子，在二次代价函数时，我们有 $\nabla_a C = (a^L - y)$，所以 (BP1) 的整个矩阵形式就变成

$\begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L) \label{eq:30}\tag{30} \end{eqnarray}$

如你所见，这个方程中的每个项都有一个很好的向量形式，所以也可以很方便地使用像 Numpy 这样的矩阵库进行计算了。

使用下一层的误差 $\delta^{l+1}$ 来表示当前层的误差 $\delta^l$：特别地，

$\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \label{eq:bp2}\tag{BP2} \end{eqnarray}$

其中 $(w^{l+1})^T$ 是 $(l+1)^{\rm th}$ 层权重矩阵 $w^{l+1}$ 的转置。这个公式看上去有些复杂，但每一个元素有很好的解释。假设我们知道 $l+1^{\rm th}$ 层的误差 $\delta^{l+1}$。当我们应用转置的权重矩阵 $(w^{l+1})^T$，我们可以凭直觉地把它看作是在沿着网络反向移动误差，给了我们度量在 $l^{\rm th}$ 层输出的误差方法。然后，我们进行 Hadamard 乘积运算 $\odot \sigma'(z^l)$。这会让误差通过 $l$ 层的激活函数反向传递回来并给出在第 $l$ 层的带权输入的误差 $\delta$。 通过组合 (BP1) 和 (BP2)，我们可以计算任何层的误差 $\delta^l$。首先使用 (BP1) 计算 $\delta^L$，然后应用方程 (BP2) 来计算$\delta^{L-1}$，然后再次用方程 (BP2) 来计算 $\delta^{L-2}$，如此一步一步地反向传播完整个网络。

代价函数关于网络中任意偏置的改变率： 就是

$\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j \label{eq:bp3}\tag{BP3} \end{eqnarray}$

这其实是，误差 $\delta^l_j$ 和偏导数值 $\partial C / \partial b^l_j$ 完全一致。这是很好的性质，因为 (BP1) 和 (BP2) 已经告诉我们如何计算 $\delta^l_j$。所以就可以将 (BP3) 简记为

$\begin{eqnarray} \frac{\partial C}{\partial b} = \delta \label{eq:31}\tag{31} \end{eqnarray}$

其中 $\delta$ 和偏置 $b$ 都是针对同一个神经元。

代价函数关于任何一个权重的改变率： 特别地，

$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \label{eq:bp4}\tag{BP4} \end{eqnarray}$

这告诉我们如何计算偏导数 $\partial C/\partial w_{jk}^l$，其中 $\delta^l$ 和 $a^{l-1}$ 这些量我们都已经知道如何计算了。方程也可以写成下面用更少下标的表示：

$\begin{eqnarray} \frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out} \label{eq:32}\tag{32} \end{eqnarray}$

其中 $a_{\rm in}$ 是输入给权重 $w$ 的神经元的激活值，$\delta_{\rm out}$ 是输出自权重 $w$ 的神经元的误差。放大看看权重 $w$，还有两个由这个权重相连的神经元，我们给出一幅图如下：

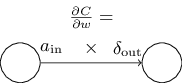
方程 (32) 的一个好的结果就是当激活值 $a_{\rm in}$ 很小，$a_{\rm in} \approx 0$，梯度 $\partial C/\partial w$ 也会趋向很小。这样，我们就说权重缓慢学习，表示在梯度下降的时候，这个权重不会改变太多。换言之，(BP4) 的一个结果就是来自低激活值神经元的权重学习会非常缓慢。

这四个公式 (BP1)--(BP4) 同样还有其它可以理解的方面。让我们从输出层开始，先看看 (BP1) 中的项 $\sigma'(z_k^l)$。回忆一下上一章中 S 型函数的图形，当 $\sigma(z^L_j)$ 近似为 $0$ 或者 $1$ 的时候 $\sigma$ 函数变得非常平。这时 $\sigma'(z^L_j) \approx 0$。所以如果输出神经元处于或者低激活值（$\approx 0$）或者高激活值（$\approx 1$）时，最终层的权重学习缓慢。这样的情形，我们常常称输出神经元已经饱和了，并且，权重学习也会终止（或者学习非常缓慢）。类似的结果对于输出神经元的偏置也是成立的。

针对前面的层，我们也有类似的观点。特别地，注意在 (BP2) 中的项 $\sigma'(z^l)$。这表示如果神经元已经接近饱和，$\delta_j^l$ 很可能变小。这就导致任何输入进一个饱和的神经元的权重学习缓慢⁴。

总结一下，我们已经学习到，如果输入神经元激活值很低，或者输出神经元已经饱和了（过高或者过低的激活值），权重会学习缓慢。

这些观测其实也不是非常出于意料的。不过，他们帮助我们完善了关于神经网络学习的背后的思维模型。而且，我们可以将这种推断方式进行推广。四个基本方程也其实对任何的激活函数都是成立的（证明中也可以看到，其实推断本身不依赖于任何具体的代价函数）所以，我们可以使用这些方程来设计有特定学习属性的激活函数。我们这里给个例子，假设我们准备选择一个（非S型）激活函数 $\sigma$ 使得 $\sigma'$ 总是正数，并且不会趋近 $0$。这会防止在原始的S型神经元饱和时学习速度下降的情况出现。在本书的后面，我们会见到这种类型的对激活函数的改变。时时回顾这四个方程(BP1)--(BP4) 可以帮助解释为何需要有这些尝试，以及尝试带来的影响。

问题

• 另一种反向传播方程的表示方式： 我已经给出了使用 Hadamard 乘积的反向传播的公式（尤其是 (BP1) 和 (BP2)）。如果你对这种特殊的乘积不熟悉，可能会有一些困惑。下面还有一种表示方式，那就是基于传统的矩阵乘法，某些读者可能会觉得很有启发。（1）证明 (BP1) 可以写成

  $\begin{eqnarray} \delta^L = \Sigma'(z^L) \nabla_a C \label{eq:33}\tag{33} \end{eqnarray}$

  其中 $\Sigma'(z^L)$ 是一个方阵，其对角线的元素是 $\sigma'(z_j^L)$，其他的元素均是 $0$。注意，这个矩阵通过一般的矩阵乘法作用在 $\nabla_a C$ 上。（2）证明(BP2) 可以写成

  $\begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \delta^{l+1} \label{eq:34}\tag{34} \end{eqnarray}$

  （3）结合（1）和（2）证明

  $\begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \ldots \Sigma'(z^{L-1}) (w^L)^T \Sigma'(z^L) \nabla_a C \label{eq:35}\tag{35} \end{eqnarray}$

  对那些习惯于这种形式的矩阵乘法的读者，(BP1) (BP2) 应该更加容易理解。而我们坚持使用 Hadamard 乘积的原因在于其更快的数值实现。

². 这里需要注意的是，只有在 $\Delta z_j^l$ 很小的时候才能够满足。我们需要假设调皮鬼只能进行微小的调整。 ↩

³. 在分类问题中，误差有时候会用作分类的错误率。如果神经网络正确分类了 96.0% 的数字，那么其误差是 4.0%。很明显，这和我们上面提及的误差的差别非常大了。在实际应用中，区分这两种含义是非常容易的。 ↩

⁴. 如果 ${w^{l+1}}^T \delta^{l+1}$ 拥有足够大的量能够补偿 $\sigma'(z_k^l)$ 的话，这里的推导就不能成立了。但是我们上面是常见的情形。 ↩