2.2 关于代价函数的两个假设

反向传播的目标是计算代价函数 $C$ 分别关于 $w$ 和 $b$ 的偏导数 $\partial C/\partial w$ 和 $\partial C / \partial b$。为了让反向传播可行，我们需要做出关于代价函数的两个主要假设。在给出这两个假设之前，我们先看看具体的一个代价函数。我们会使用上一章使用的二次代价函数（参见方程 (6)）。按照上一节给出的表示，二次代价函数有下列形式：

$\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2 \label{eq:26}\tag{26} \end{eqnarray}$

其中 $n$ 是训练样本的总数；求和运算遍历了每个训练样本 $x$；$y = y(x)$ 是对应的目标输出；$L$ 表示网络的层数；$a^L = a^L(x)$ 是当输入是 $x$ 时的网络输出的激活值向量。

好了，为了应用反向传播，我们需要对代价函数 $C$ 做出什么样的前提假设呢？第一个假设就是代价函数可以被写成一个在每个训练样本 $x$ 上的代价函数 $C_x$ 的均值 $C=\frac{1}{n} \sum_x C_x$。这是关于二次代价函数的例子，其中对每个独立的训练样本其代价是 $C_x = \frac{1}{2} ||y-a^L||^2$。这个假设对书中提到的其他任何一个代价函数也都是必须满足的。

需要这个假设的原因是反向传播实际上是对一个独立的训练样本计算了 $\partial C_x/\partial w$ 和 $\partial C_x/\partial b$。然后我们通过在所有训练样本上进行平均化获得 $\partial C/\partial w$ 和 $\partial C/\partial b$。实际上，有了这个假设，我们会认为训练样本 $x$ 已经被固定住了，丢掉了其下标，将代价函数 $C_x$ 看做 $C$。最终我们会把下标加上，现在为了简化表示其实没有这个必要。

第二个假设就是代价可以写成神经网络输出的函数：

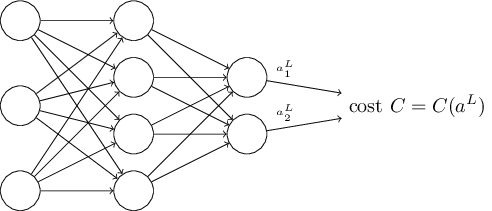
例如，二次代价函数满足这个要求，因为对于一个单独的训练样本 $x$ 其二次代价函数可以写作：

$\begin{eqnarray} C = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2 \label{eq:27}\tag{27} \end{eqnarray}$

这是输出的激活值的函数。当然，这个代价函数同样还依赖于目标输出 $y$，你可能奇怪为什么我们不把代价也看作一个 $y$ 的函数。记住，输入的训练样本 $x$ 是固定的，所以输出 $y$ 同样是一个固定的参数。尤其是它并不是可以随意通过改变权重和偏置来改变的，也就是说，这不是神经网络学习的对象。所以，将 $C$ 看成仅有输出激活值 $a^L$ 的函数才是合理的，而 $y$ 仅仅是帮助定义函数的参数而已。