2.1 热身：神经网络中使用矩阵快速计算输出的方法

在讨论反向传播前，我们先熟悉一下基于矩阵的算法来计算网络的输出。事实上，我们在上一章的最后已经能够看到这个算法了，但是我在那里很快地略过了，所以现在让我们仔细讨论一下。特别地，这样能够用相似的场景帮助我们熟悉在反向传播中使用的矩阵表示。

我们首先给出网络中权重的清晰定义。我们使用 $w^l_{jk}$ 表示从 $(l-1)^{\rm th}$ 层的 $k^{\rm th}$ 个神经元到 $l^{\rm th}$ 层的 $j^{\rm th}$ 个神经元的链接上的权重。例如，下图给出了网络中第二层的第四个神经元到第三层的第二个神经元的链接上的权重：

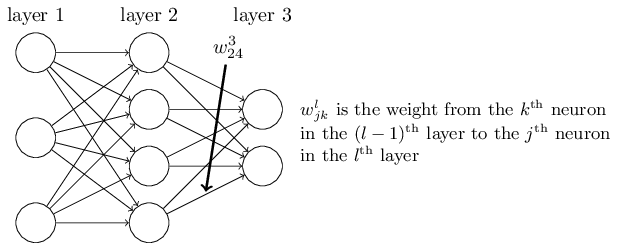
这样的表示粗看比较奇怪，需要花一点时间消化。但是，后面你会发现这样的表示会比较方便也很自然。奇怪的一点其实是下标 $j$ 和 $k$ 的顺序。你可能觉得反过来更加合理。但我接下来会告诉你为什么要这样做。

我们对网络的偏置和激活值也会使用类似的表示。显式地，我们使用 $b^l_j$ 表示在$l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的偏置，使用 $a^l_j$ 表示 $l^{\rm th}$ 层第 $j^{\rm th}$ 个神经元的激活值。下面的图清楚地解释了这样表示的含义：

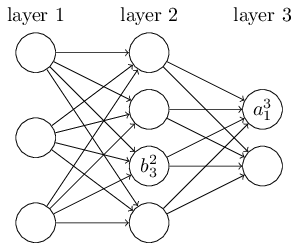
有了这些表示，$l^{\rm th}$ 层的第 $j^{\rm th}$ 个神经元的激活值 $a^{l}_j$ 就和 $(l-1)^{\rm th}$ 层的激活值通过方程关联起来了（对比公式 (4) 和上一章的讨论）：

$\begin{eqnarray} a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right) \label{eq:23}\tag{23} \end{eqnarray}$

其中求和是在 $(l-1)^{\rm th}$ 层的所有 $k$ 个神经元上进行的。为了用矩阵的形式重写这个表达式，我们对每一层 $l$ 都定义一个权重矩阵 $w^l$。权重矩阵 $w^l$ 的元素正是连接到 $l^{\rm th}$ 层神经元的权重，更确切地说，在第 $j^{\rm th}$ 行第 $k^{\rm th}$ 列的元素是 $w^l_{jk}$。类似的，对每一层 $l$，定义一个偏置向量，$b^l$。你已经猜到这些如何工作了 —— 偏置向量的每个元素其实就是前面给出的 $b^l_j$，每个元素对应于 $l^{\rm th}$ 层的每个神经元。最后，我们定义激活向量 $a^l$，其元素是那些激活值 $a^l_j$。

最后我们需要引入向量化函数（如 $\sigma$）来按照矩阵形式重写公式 (23)。在上一章，我们其实已经碰到向量化了，其含义就是作用函数（如 $\sigma$）到向量 $v$ 中的每个元素。我们使用 $\sigma(v)$ 表示这种按元素进行的函数作用。所以，$\sigma(v)$ 的每个元素其实满足 $\sigma(v)_j = \sigma(v_j)$。给个例子，如果我们的作用函数是 $f(x) = x^2$，那么向量化的 $f$ 的函数作用就起到下面的效果：

$\begin{eqnarray} f\left(\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \right) = \left[ \begin{array}{c} f(2) \\ f(3) \end{array} \right] = \left[ \begin{array}{c} 4 \\ 9 \end{array} \right] \label{eq:24}\tag{24} \end{eqnarray}$

也就是说，向量化的 $f$ 仅仅是对向量的每个元素进行了平方运算。

了解了这些表示，方程 (23) 就可以写成下面这种美妙而简洁的向量形式了：

$\begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l) \label{eq:25}\tag{25} \end{eqnarray}$

这个表达式给出了一种更加全局的思考每层的激活值和前一层激活值的关联方式：我们仅仅用权重矩阵作用在激活值上，然后加上一个偏置向量，最后作用 $\sigma$ 函数¹。这种全局的观点相比神经元层面的观点常常更加简明（没有更多的索引下标了！）。把它看做是在保留清晰认识的前提下逃离下标困境的方法。在实践中，表达式同样很有用，因为大多数矩阵库提供了实现矩阵乘法、向量加法和向量化的快速方法。实际上，上一章的代码其实已经隐式使用了这种表达式来计算网络行为。

在使用方程 (25) 计算 $a^l$ 的过程中，我们计算了中间量 $z^l \equiv w^l a^{l-1}+b^l$。这个量其实是非常有用的：我们称 $z^l$ 为 $l$ 层神经元的带权输入。在本章后面，我们会充分利用带权输入 $z^l$。方程 (25) 有时候会以带权输入的形式写作 $a^l = \sigma(z^l)$。同样要指出的是 $z^l$ 的每个元素是 $z^l_j = \sum_k w^l_{jk} a^{l-1}_k+b^l_j$，其实 $z^l_j$ 就是第 $l$ 层第 $j$ 个神经元的激活函数的带权输入。

¹. 其实，这就是让我们使用之前的矩阵下标 $w_{jk}^l$ 表示的初因。如果我们使用 $j$ 来索引输入神经元，$k$ 索引输出神经元，那么在方程 (25) 中我们需要将这里的矩阵换做其转置。这是一个小的改变，但是令人困惑，这会使得我们无法自然地讲出（思考）“应用权重矩阵到激活值上”这样的简单的表达。 ↩