1.4 一个简单的分类手写数字的网络
定义神经网络后,让我们回到手写识别上来。我们可以把识别手写数字的问题分成两个子问题。首先,我们希望有个方式把包含许多数字的图像分成一系列单独的图像,每个包含单个数字。例如,我们想要把图像
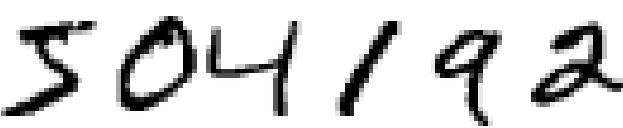
分成六个单独的图像,

我们人类可以很容易解决这个分割的问题,但是对于计算机程序来说却是个挑战。一旦图像被分割,那么程序需要把每个单独的数字分类。例如,我们想要我们的程序能识别上面的第一个数字是 。
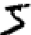
我们将专注于编程解决第二个问题,分类单独的数字。这样是因为,一旦你有分类单独数字的有效方法,分割问题是不难解决的。有很多途径可以解决分割的问题。一种方法是尝试不同的分割方式,用数字分类器对每一个切分片段打分。如果数字分类器对每一个片段的置信度都比较高,那么这个分割方式就能得到较高的分数;如果数字分类器在一或多个片段中出现问题,那么这种分割方式就会得到较低的分数。这种方法的思想是,如果分类器有问题,那么很可能是由于图像分割出错导致的。这种思想以及它的变化形式能够比较好地解决分割问题。因此,与其关心分割问题,我们不如把精力集中在设计一个神经网络来解决更有趣、更困难的问题,即手写数字的识别。
我们将使用一个三层神经网络来识别单个数字:
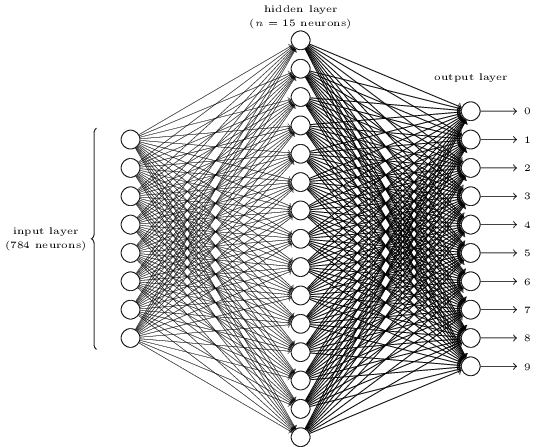
网络的输入层包含给输入像素的值进行编码的神经元。就像下一节会讨论的,我们给网络的训练数据会有很多扫描得到的 的手写数字的图像组成,所有输入层包含有 个神经元。为了简化,上图中我已经忽略了 中大部分的输入神经元。输入像素是灰度级的,值为 表示白色,值为 表示黑色,中间数值表示逐渐暗淡的灰色。
网络的第二层是一个隐藏层。我们用 来表示神经元的数量,我们将给 实验不同的数值。示例中用一个小的隐藏层来说明,仅仅包含 个神经元。
网络的输出层包含有 个神经元。如果第一个神经元激活,即输出 ,那么表明网络认为数字是一个 。如果第二个神经元激活,就表明网络认为数字是一个 。依此类推。更确切地说,我们把输出神经元的输出赋予编号 到 ,并计算出那个神经元有最高的激活值。比如,如果编号为 的神经元激活,那么我们的网络会猜到输入的数字是 。其它神经元相同。
你可能会好奇为什么我们用 个输出神经元。毕竟我们的任务是能让神经网络告诉我们哪个数字( )能和输入图片匹配。一个看起来更自然的方式就是使用 个输出神经元,把每一个当做一个二进制值,结果取决于它的输出更靠近 还是 。四个神经元足够编码这个问题了,因为 大于 种可能的输入。为什么我们反而要用 个神经元呢?这样做难道效率不低吗?最终的判断是基于经验主义的:我们可以实验两种不同的网络设计,结果证明对于这个特定的问题而言, 个输出神经元的神经网络比 个的识别效果更好。但是令我们好奇的是为什么使用 个输出神经元的神经网络更有效呢。有没有什么启发性的方法能提前告诉我们用 个输出编码比使用 个输出编码更有好呢?
为了理解为什么我们这么做,我们需要从根本原理上理解神经网络究竟在做些什么。首先考虑有 个神经元的情况。我们首先考虑第一个输出神经元,它告诉我们一个数字是不是 。它能那么做是因为可以权衡从隐藏层来的信息。隐藏层的神经元在做什么呢?假设隐藏层的第一个神经元只是用于检测如下的图像是否存在:

为了达到这个目的,它通过对此图像对应部分的像素赋予较大权重,对其它部分赋予较小的权重。同理,我们可以假设隐藏层的第二,第三,第四个神经元是为检测下列图片是否存在:

就像你能猜到的,这四幅图像组合在一起构成了前面显示的一行数字图像中的 :

如果所有隐藏层的这四个神经元被激活那么我们就可以推断出这个数字是 。当然,这不是我们推断出 的唯一方式 —— 我们能通过很多其他合理的方式得到 (举个例子来说, 通过上述图像的转换,或者稍微变形)。但至少在这个例子中我们可以推断出输入的数字是 。
假设神经网络以上述方式运行,我们可以给出一个貌似合理的理由去解释为什么用 个输出而不是 个。如果我们有 个输出,那么第一个输出神经元将会尽力去判断数字的最高有效位是什么。把数字的最高有效位和数字的形状联系起来并不是一个简单的问题。很难想象出有什么恰当的历史原因,一个数字的形状要素会和一个数字的最高有效位有什么紧密联系。
上面我们说的只是一个启发性的方法。没有什么理由表明这个三层的神经网络必须按照我所描述的方式运行,即隐藏层是用来探测数字的组成形状。可能一个聪明的学习算法将会找到一些合适的权重能让我们仅仅用 个输出神经元就行。但是这个启发性的方法通常很有效,它会节省你大量时间去设计一个好的神经网络结构。
练习
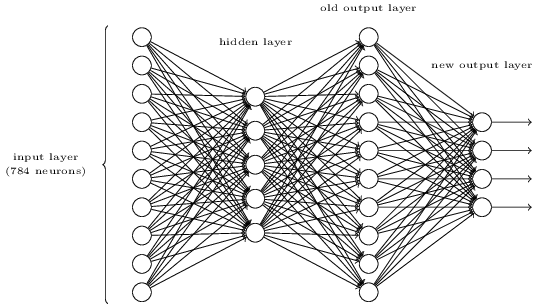
- 通过在上述的三层神经网络加一个额外的一层就可以实现按位表示数字。额外的一层把原来的输出层转化为一个二进制表示,如下图所示。为新的输出层寻找一些合适的权重和偏置。假定原先的3层神经网络在第三层得到正确输出(即原来的输出层)的激活值至少是 ,得到错误的输出的激活值至多是 。